Hướng dẫn sử dụng công cụ mô phỏng mã hóa và giải mã DES

Công cụ này mô phỏng quy trình mã hóa và giải mã dữ liệu bằng thuật toán DES (Data Encryption Standard). Giao thức Diffie-Hellman được sử dụng để trao đổi khóa an toàn, kết hợp với chữ ký số để xác minh danh tính, ngăn chặn tấn công man-in-the-middle (MITM). Người dùng nhập hai số bí mật (a và b) để tạo khóa chung, sau đó khóa này được băm bằng MD5 (lấy 16 ký tự HEX đầu tiên) để tạo khóa DES. Quy trình bao gồm:

  • Bước 1: Trao đổi khóa công khai Diffie-Hellman.
  • Bước 2: Tạo cặp khóa RSA cho chữ ký số.
  • Bước 3: Xác minh danh tính người gửi qua chữ ký số.
  • Bước 4: Tạo khóa chung bằng Diffie-Hellman.
  • Bước 5: Băm khóa chung bằng MD5 để tạo khóa DES.
  • Bước 6: Mã hóa hoặc giải mã dữ liệu bằng DES, hỗ trợ định dạng ASCII, HEX và BIN.
Lưu ý: Việc nhập cả hai số bí mật a và b chỉ dành cho mục đích mô phỏng. Trong thực tế, mỗi bên chỉ giữ số bí mật của mình và trao đổi khóa công khai qua kênh liên lạc.

1. Tạo khóa với Diffie-Hellman

Công cụ cho phép mô phỏng giao thức Diffie-Hellman bằng cách nhập cả hai số bí mật (a và b) để tính toán khóa công khai và khóa chung. Quy trình bao gồm:

  • Bước 1: Nhập tham số Diffie-Hellman
    • Nhập số nguyên tố p và số nguyên g (generator). Công cụ có thể cung cấp giá trị mặc định.
    • Nhập số bí mật của hai bên: a và b.
    • Ví dụ:
      Tham số Giá trị
      p 23
      g 5
      Số bí mật a 18
      Số bí mật b 7
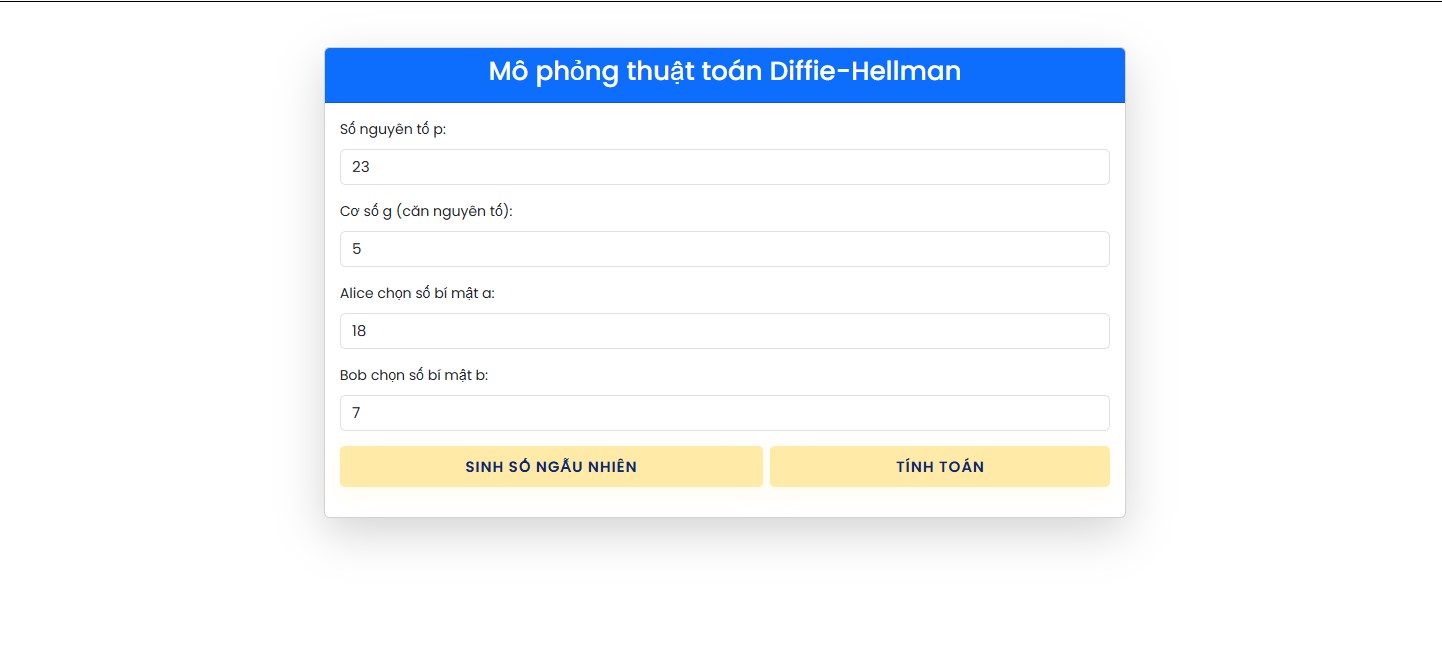    Giao diện nhập tham số Diffie-Hellman
    Giao diện nhập tham số Diffie-Hellman trong công cụ.
  • Bước 2: Tính khóa công khai và khóa chung
    • Khóa công khai:
      Khóa Công thức Ví dụ
      A g^a mod p 5^18 mod 23 = 6
      B g^b mod p 5^7 mod 23 = 17
    • Khóa chung:
      Khóa Công thức Ví dụ
      K A^b mod p = B^a mod p 17^18 mod 23 = 6^7 mod 23 = 3
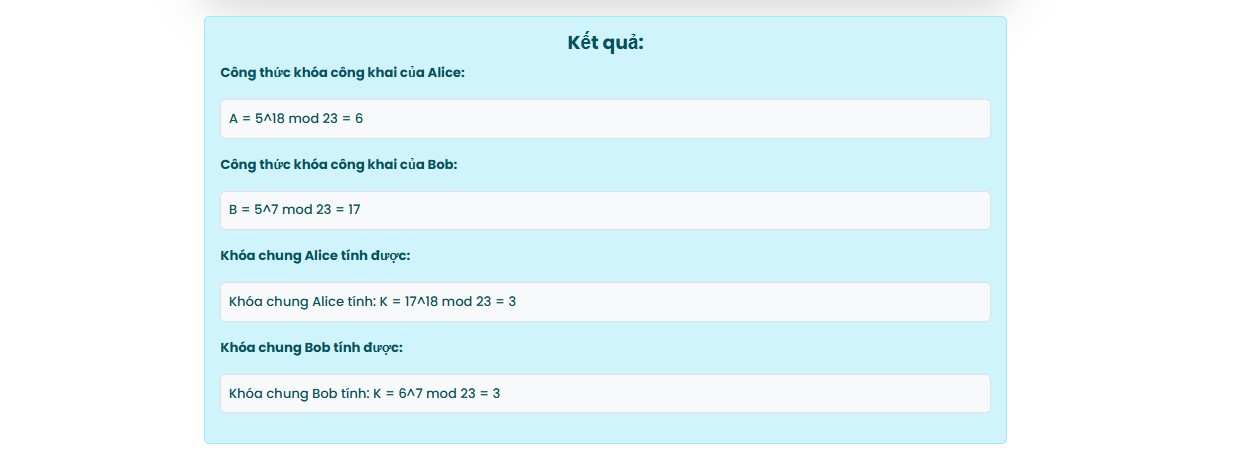
Giao diện tính toán Diffie-Hellman
Lưu ý: Trong mô phỏng, bạn nhập cả a và b để thấy toàn bộ quy trình từ tính khóa công khai đến khóa chung. Trong thực tế, b là bí mật của đối phương và không được chia sẻ, khóa công khai trước khi gửi cho người nhận cần phải được thực hiện cùng chữ ký số để xác minh.

2. Tạo cặp khóa RSA cho chữ ký số

Trước khi xác minh chữ ký số, cần tạo cặp khóa RSA gồm khóa công khai và khóa riêng để sử dụng trong quá trình ký và xác minh danh tính. Khóa riêng được giữ bí mật, còn khóa công khai được chia sẻ để xác minh chữ ký.

  • Bước 1: Tạo cặp khóa RSA
    • Chọn hai số nguyên tố lớn p và q (ví dụ: p = 61, q = 53).
    • Tính n = p * q và hàm Euler φ(n) = (p-1) * (q-1).
    • Chọn số nguyên e sao cho 1 < e < φ(n) và e nguyên tố cùng nhau với φ(n).
    • Tính d sao cho d * e ≡ 1 mod φ(n).
    • Kết quả:
      Tham số Ví dụ
      n 61 * 53 = 3233
      φ(n) (61-1) * (53-1) = 3120
      Khóa công khai (e, n) = (17, 3233)
      Khóa riêng (d, n) = (2753, 3233)
  • Bước 2: Lưu và chia sẻ khóa
    • Lưu khóa riêng (d, n) ở nơi an toàn, không chia sẻ.
    • Chia sẻ khóa công khai (e, n) với đối phương để họ sử dụng trong xác minh chữ ký.
  • Bước 3: Nhấn nút "Tạo khóa RSA"
    • Công cụ sẽ hiển thị cặp khóa RSA (e, n và d, n).
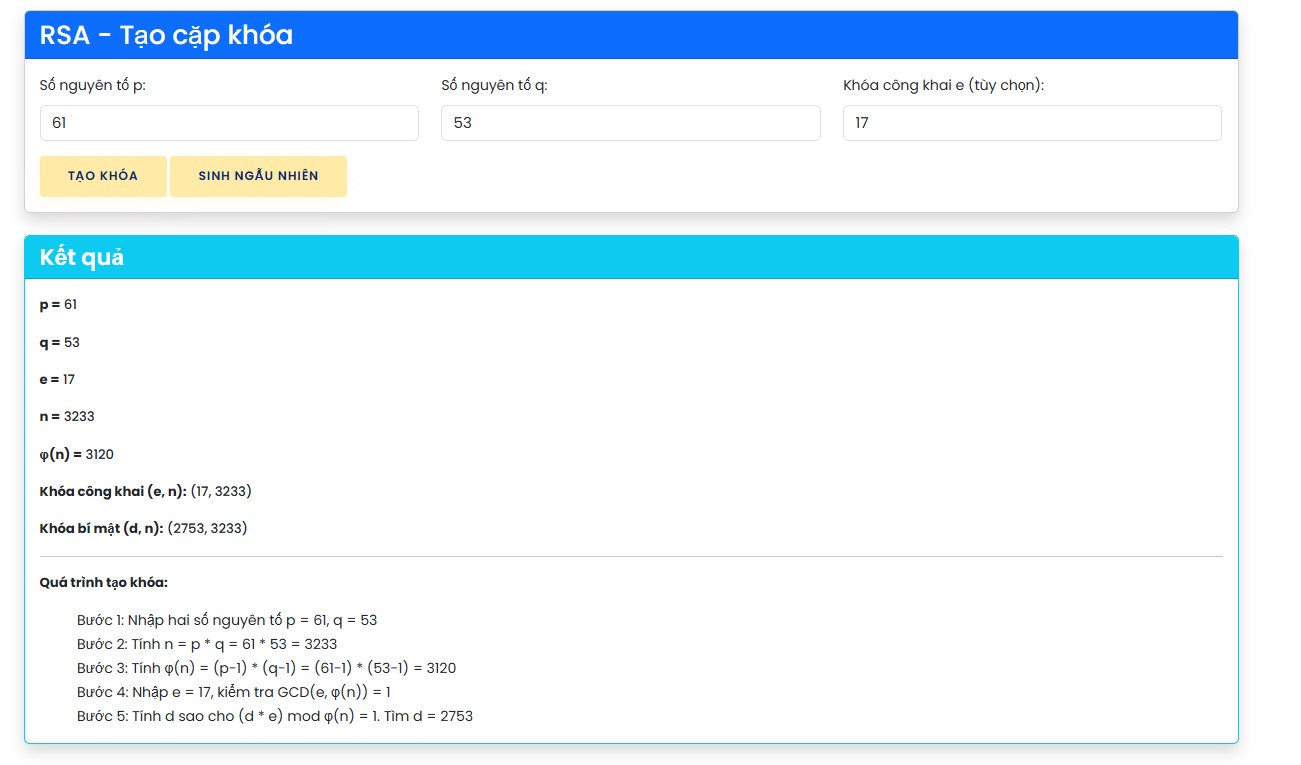
Giao diện tính toán RSA
Lưu ý: Trong thực tế, các số nguyên tố p và q phải rất lớn (thường 2048 bit hoặc hơn) để đảm bảo an toàn. Trong mô phỏng, các số nhỏ được dùng để đơn giản hóa.

3. Xác minh người gửi bằng chữ ký số

Để đảm bảo khóa công khai từ A gửi đến B đáng tin cậy, công cụ sử dụng chữ ký số để xác minh danh tính.

  • Bước 1: Nhận chữ ký số
    • Người gửi (A) sẽ gửi khóa công khai kèm chữ ký số (tạo bằng thuật toán RSA với khóa riêng) cho người nhận (B).
    • Chữ ký số (S) là 1 giá trị được tạo bằng cách ký thông điệp (trong ví dụ này thông điệp là khóa công khai của giao thức Diffie Helman ở phần 1)
    Ký số

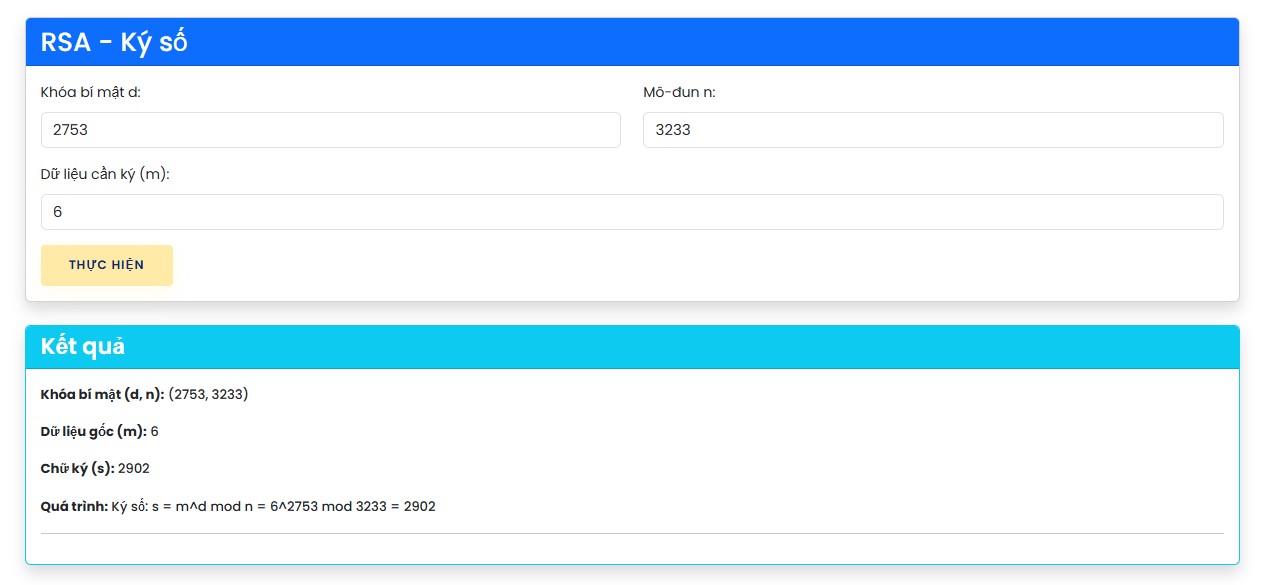
    Kết quả nhận được: S = m^d mod n = 6^2753 mod 3233 = 2902 (đây là chữ ký)

    Người gửi (A) sẽ gửi khóa công khai diffie-helman và chữ ký cho (B): (6,2902)

  • Bước 2: Nhập thông tin xác minh
    • Người nhận B sau khi nhận được thông điệp (khóa công khai diffie-helman) và chữ ký từ A (6,2902) sẽ kiểm xác minh bằng khóa công khai của A.
    • Ví dụ:
      Tham số Giá trị
      Thông điệp cần xác minh 6
      Chữ ký số 2902
      Khóa công khai RSA (e, n) = (17, 3233)
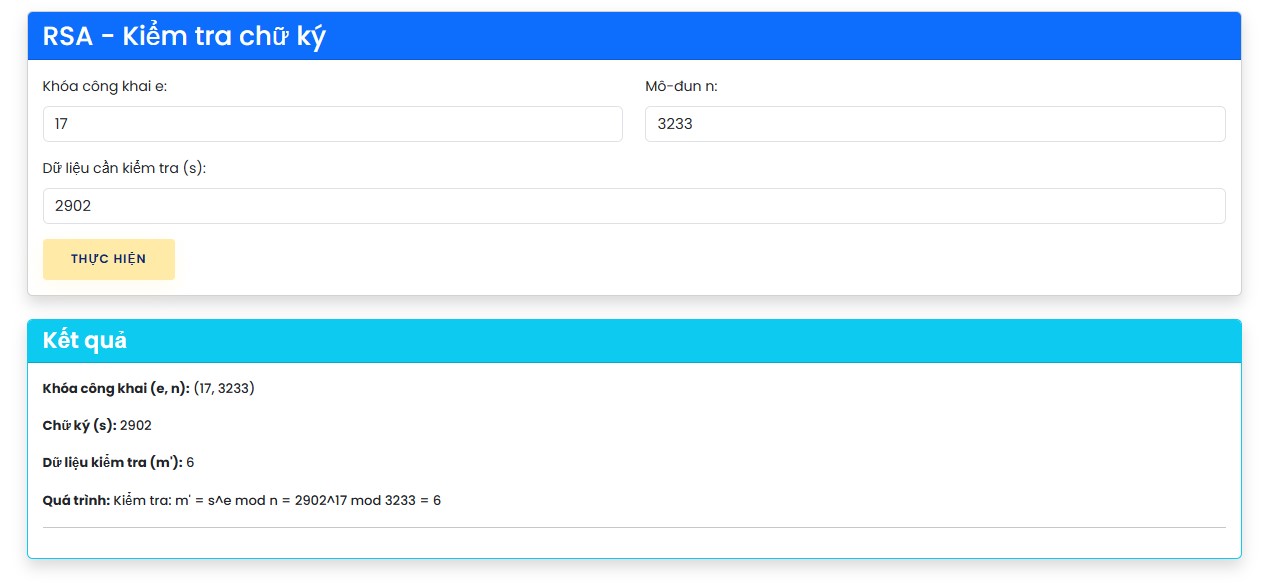
  • Bước 3: Thực hiện kiểm tra Xác minh

    Kết quả nhận được: m = s^e mod n = 2902^17 mod 3233 = 6 (kết quả sau khi xác minh chữ ký trùng khớp với nội dung mà A gửi) -> thông điệp không bị thay đổi

Lưu ý: Nếu xác minh thất bại (kết quả khi xác minh chữ ký không trùng khớp với thông điệp), thì không sử dụng vì có thể thông điệp đã bị tấn công MITM.

4. Tính toán và băm khóa chung

Sau khi xác minh B, công cụ băm khóa chung bằng MD5 để tạo khóa DES.

  • Bước 1: Khóa chung
    • Khóa chung K đã được tính ở bước 1 (K = 3).
  • Bước 2: Băm khóa chung bằng MD5
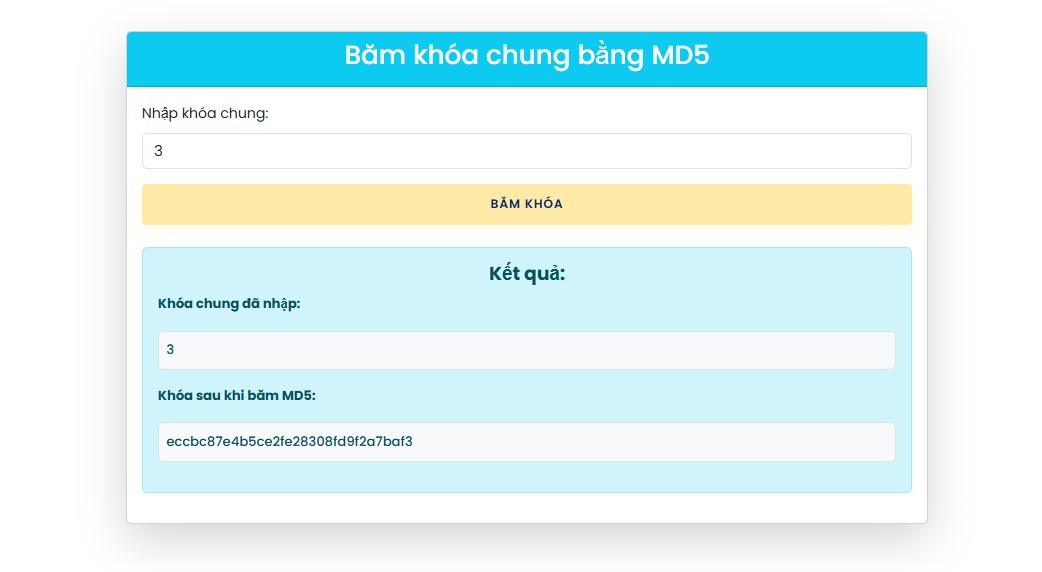
    • Công cụ băm K bằng MD5 (vì thuật toán DES cần dữ liệu đầu vào có độ dài 64 bit tương ứng 8 byte) lấy 16 ký tự HEX đầu tiên (8 byte) làm khóa DES.
      • Hàm băm MD5
    • Thao tác Giá trị
      Khóa chung K 3
      MD5(K) eccbc87e4b5ce2fe28308fd9f2a7baf3
      Khóa DES eccbc87e4b5ce2fe

5. Mã hóa dữ liệu với DES

Sử dụng khóa DES để mã hóa thông điệp. Quy trình bao gồm:

  • Bước 1: Nhập thông điệp (Plaintext)
    • Chọn định dạng: ASCII, HEX, hoặc BIN.
    • Ví dụ:
      Định dạng Giá trị
      ASCII Là dạng chữ (Chỉ hỗ trợ tiếng Anh) như "Hello".
      HEX Là dạng mã hóa thành số kiểu hệ 16, từ 0-9 và A-F. Ví dụ: eccbc87e4b5ce2fe
      BIN Là dạng chỉ dùng 0 và 1. Ví dụ: 1110110011001011110010000111111001001011010111001110001011111110
  • Bước 2: Nhập khóa DES
    • Chọn định dạng: ASCII, HEX, hoặc BIN.
    • Nhập khóa DES từ bước 4 eccbc87e4b5ce2fe khóa này ở dạng HEX.
  • Bước 3: Nhấn nút "Xử lý dữ liệu"
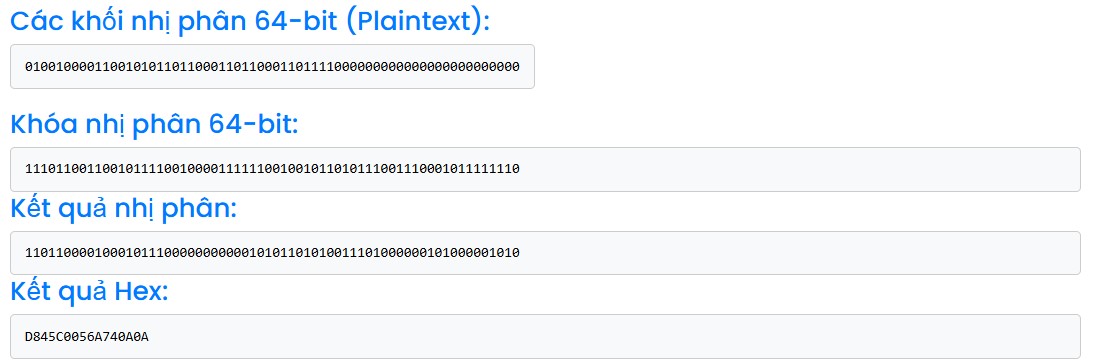
    Mã hóa DES Kết quả mã hóa DES
    • Đầu vào Giá trị
      Thông điệp cần mã hóa Hello (Ascii).
      Khóa eccbc87e4b5ce2fe (Hex)
      Kết quả: D845C0056A740A0A (Hex)
      1101100001000101110000000000010101101010011101000000101000001010 (BIN)
Lưu ý: Thông điệp nếu dài hơn 64 bit sẽ được chia thành các khối 64 bit (các khối không đủ sẽ được padding). Kết quả sau khi mã hóa sẽ ở dạng Hex hoặc Bin, dùng dạng nào để giải mã cũng được.

6. Giải mã dữ liệu với DES

Sử dụng khóa DES để giải mã bản mã. Quy trình bao gồm:

  • Bước 1: Nhập bản mã (Ciphertext)
    • Chọn định dạng: HEX hoặc BIN.
    • D845C0056A740A0A (HEX).
  • Bước 2: Nhập khóa DES
    • Nhập khóa DES giống bước mã hóa eccbc87e4b5ce2fe.
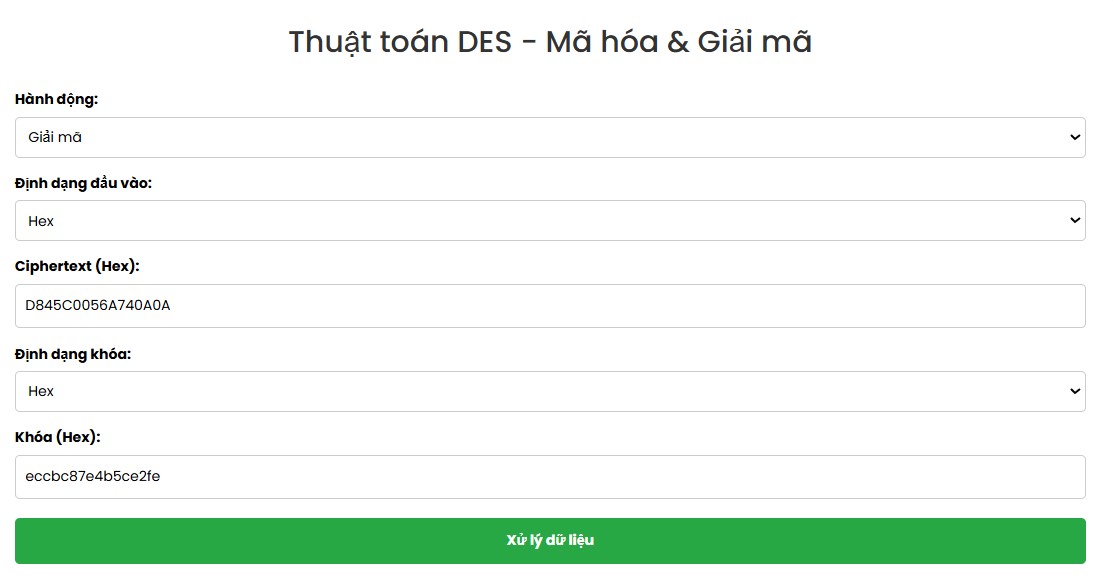
  • Bước 3: Nhấn nút "Xử lý dữ liệu"
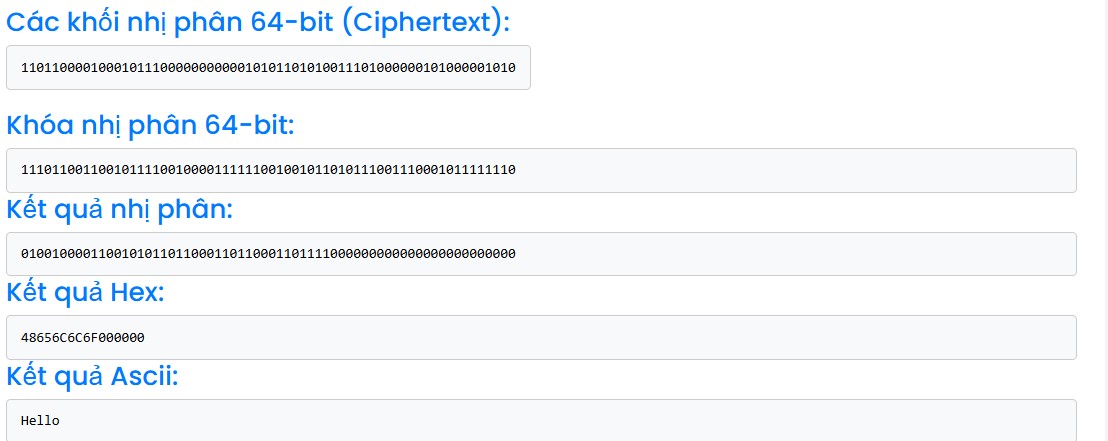
    Giải mã thuật toán DES Kết quả giải mã DES
    • Đầu vào Giá trị
      Thông điệp cần giải mã D845C0056A740A0A (Hex).
      Khóa eccbc87e4b5ce2fe (Hex)
      Kết quả: 48656C6C6F000000 (Hex)
      0100100001100101011011000110110001101111000000000000000000000000 (BIN)
      Hello (Ascii)

7. Minh họa toàn bộ quy trình

Dưới đây là toàn bộ quy trình:

Thao tác Đầu vào Đầu ra
Tạo khóa Diffie-Hellman p = 23, g = 5
Số bí mật: a = 18, b = 7 		Khóa công khai: A = 6, B = 17
Khóa chung: K = 3
Tạo khóa RSA Số nguyên tố: p = 61, q = 53
e = 17 		Khóa công khai: (e, n) = (17, 3233)
Khóa riêng: (d, n) = (2753, 3233)
Tạo chữ ký số Khóa bí mật (RSA) của A = 2753, dữ liệu cần ký là khóa công khai (Diffie-helman) của A = 6 S = m^d mod n = 6^2753 mod 3233 = 2902
Xác minh chữ ký Khóa công khai (RSA) của A = (17,3233), chữ ký số S = 2902 m = s^e mod n = 2902^17 mod 3233 = 6 -> Xác minh thành công
Tạo khóa DES Khóa chung: K = 3 Khóa DES: eccbc87e4b5ce2fe (16 ký tự HEX đầu của MD5)
Mã hóa Bản rõ: Hello (ASCII)
Khóa: eccbc87e4b5ce2fe (HEX) 		Bản mã: D845C0056A740A0A (HEX)
Giải mã Bản mã: D845C0056A740A0A (HEX)
Khóa: eccbc87e4b5ce2fe (HEX)
 Bản rõ: Hello (ASCII)

8. Lưu ý quan trọng

  • Đây là công cụ mô phỏng, cho phép nhập cả a và b để minh họa Diffie-Hellman. Trong thực tế, chỉ chia sẻ khóa công khai (A, B), không chia sẻ số bí mật.
  • Khóa RSA phải được tạo với số nguyên tố lớn (2048 bit hoặc hơn) để đảm bảo an toàn trong thực tế.
  • Luôn xác minh chữ ký số để đảm bảo khóa công khai là đáng tin cậy.
  • MD5 được dùng trong mô phỏng để đơn giản hóa, nhưng không an toàn cho ứng dụng thực tế.

Quay lại trang chủ

Web hosting by Somee.com